Information

The Information module of MIToS defines types and functions useful to calculate information measures (e.g. Mutual Information (MI) and Entropy) over a Multiple Sequence Alignment (MSA). This module was designed to count Residues (defined in the MSA module) in special contingency tables (as fast as possible) and to derive probabilities from these counts. Also, includes methods for applying corrections to those tables, e.g. pseudocounts and pseudo frequencies. Finally, Information allows to use these probabilities and counts to estimate information measures and other frequency based values.

using MIToS.Information # to load the Information module

Features

Estimate multi dimensional frequencies and probability tables from sequences, MSAs, etc...
Correction for small number of observations
Correction for data redundancy on a MSA
Estimate information measures
Calculate corrected mutual information between residues

Information

Counting residues

MIToS Information module defines a multidimensional ContingencyTable type and two types wrapping it, Counts and Probabilities, to store occurrences or probabilities. The ContingencyTable type stores the contingency matrix, its marginal values and total. These types are parametric, taking three ordered parameters:

T : The type used for storing the counts or probabilities, e.g. Float64. It's possible to use BigFloat if more precision it's needed.
N : It's the dimension of the table and should be an Int.
A : This should be a type, subtype of ResidueAlphabet, i.e.: UngappedAlphabet, GappedAlphabet or ReducedAlphabet.

Note

ContingencyTable can be used for storing probabilities or counts. The wrapper types Probabilities and Counts are mainly intended to dispatch in methods that need to know if the matrix has probabilities or counts, e.g. entropy. In general, the use of ContingencyTable is recommended over the use of Probabilities and Counts.

In this way, a matrix for storing pairwise probabilities of residues (without gaps) can be initialized using:

using MIToS.Information

Pij = ContingencyTable(Float64, Val{2}, UngappedAlphabet())

MIToS.Information.ContingencyTable{Float64, 2, MIToS.MSA.UngappedAlphabet} : 

table : 20×20 Named Matrix{Float64}
Dim_1 ╲ Dim_2 │   A    R    N    D    C    Q  …    P    S    T    W    Y    V
──────────────┼──────────────────────────────────────────────────────────────
A             │ 0.0  0.0  0.0  0.0  0.0  0.0  …  0.0  0.0  0.0  0.0  0.0  0.0
R             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
N             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
D             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
C             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
Q             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
E             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
G             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
⋮                 ⋮    ⋮    ⋮    ⋮    ⋮    ⋮  ⋱    ⋮    ⋮    ⋮    ⋮    ⋮    ⋮
M             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
F             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
P             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
S             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
T             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
W             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
Y             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
V             │ 0.0  0.0  0.0  0.0  0.0  0.0  …  0.0  0.0  0.0  0.0  0.0  0.0

marginals : 20×2 Named Matrix{Float64}
Residue ╲ Dim │ Dim_1  Dim_2
──────────────┼─────────────
A             │   0.0    0.0
R             │   0.0    0.0
N             │   0.0    0.0
D             │   0.0    0.0
C             │   0.0    0.0
Q             │   0.0    0.0
E             │   0.0    0.0
G             │   0.0    0.0
⋮                   ⋮      ⋮
M             │   0.0    0.0
F             │   0.0    0.0
P             │   0.0    0.0
S             │   0.0    0.0
T             │   0.0    0.0
W             │   0.0    0.0
Y             │   0.0    0.0
V             │   0.0    0.0

total : 0.0

[High level interface] It is possible to use the functions count and probabilities to easily calculate the frequencies of sequences or columns of a MSA, where the number of sequences/columns determine the dimension of the resulting table.

using MIToS.Information
using MIToS.MSA # to use res"..." to create Vector{Residue}

column_i = res"AARANHDDRDC-"
column_j = res"-ARRNHADRAVY"
#   Nij[R,R] =   1     1   = 2

Nij = count(column_i, column_j)

MIToS.Information.Counts{Float64, 2, MIToS.MSA.UngappedAlphabet} wrapping a MIToS.Information.ContingencyTable{Float64, 2, MIToS.MSA.UngappedAlphabet} : 

table : 20×20 Named Matrix{Float64}
Dim_1 ╲ Dim_2 │   A    R    N    D    C    Q  …    P    S    T    W    Y    V
──────────────┼──────────────────────────────────────────────────────────────
A             │ 1.0  1.0  0.0  0.0  0.0  0.0  …  0.0  0.0  0.0  0.0  0.0  0.0
R             │ 0.0  2.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
N             │ 0.0  0.0  1.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
D             │ 2.0  0.0  0.0  1.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
C             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  1.0
Q             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
E             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
G             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
⋮                 ⋮    ⋮    ⋮    ⋮    ⋮    ⋮  ⋱    ⋮    ⋮    ⋮    ⋮    ⋮    ⋮
M             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
F             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
P             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
S             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
T             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
W             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
Y             │ 0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0
V             │ 0.0  0.0  0.0  0.0  0.0  0.0  …  0.0  0.0  0.0  0.0  0.0  0.0

marginals : 20×2 Named Matrix{Float64}
Residue ╲ Dim │ Dim_1  Dim_2
──────────────┼─────────────
A             │   2.0    3.0
R             │   2.0    3.0
N             │   1.0    1.0
D             │   3.0    1.0
C             │   1.0    0.0
Q             │   0.0    0.0
E             │   0.0    0.0
G             │   0.0    0.0
⋮                   ⋮      ⋮
M             │   0.0    0.0
F             │   0.0    0.0
P             │   0.0    0.0
S             │   0.0    0.0
T             │   0.0    0.0
W             │   0.0    0.0
Y             │   0.0    0.0
V             │   0.0    1.0

total : 10.0

You can use sum to get the stored total:

sum(Nij) # There are 12 Residues, but 2 are gaps

10.0

Contingency tables can be indexed using Int or Residues:

Nij[2, 2] # Use Int to index the table

2.0

Nij[Residue('R'), Residue('R')] # Use Residue to index the table

2.0

Warning

The number makes reference to the specific index in the table e.g [2,2] references the second row and the second column. The use of the number used to encode the residue to index the table is dangerous. The equivalent index number of a residue depends on the used alphabet and Int(Residue('X')) will be always out of bounds.

Indexing with Residues works as expected. It uses the alphabet of the contingency table to find the index of the Residue.

using MIToS.Information
using MIToS.MSA

alphabet = ReducedAlphabet("(AILMV)(NQST)(RHK)(DE)(FWY)CGP")

column_i = res"AARANHDDRDC-"
column_j = res"-ARRNHADRAVY"
#   Fij[R,R] =   1  1  1   = 3 # RHK

Fij = count(column_i, column_j, alphabet=alphabet)

MIToS.Information.Counts{Float64, 2, MIToS.MSA.ReducedAlphabet} wrapping a MIToS.Information.ContingencyTable{Float64, 2, MIToS.MSA.ReducedAlphabet} : 

table : 8×8 Named Matrix{Float64}
Dim_1 ╲ Dim_2 │ AILMV   NQST    RHK     DE    FWY      C      G      P
──────────────┼───────────────────────────────────────────────────────
AILMV         │   1.0    0.0    1.0    0.0    0.0    0.0    0.0    0.0
NQST          │   0.0    1.0    0.0    0.0    0.0    0.0    0.0    0.0
RHK           │   0.0    0.0    3.0    0.0    0.0    0.0    0.0    0.0
DE            │   2.0    0.0    0.0    1.0    0.0    0.0    0.0    0.0
FWY           │   0.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0
C             │   1.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0
G             │   0.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0
P             │   0.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0

marginals : 8×2 Named Matrix{Float64}
Residue ╲ Dim │ Dim_1  Dim_2
──────────────┼─────────────
AILMV         │   2.0    4.0
NQST          │   1.0    1.0
RHK           │   3.0    4.0
DE            │   3.0    1.0
FWY           │   0.0    0.0
C             │   1.0    0.0
G             │   0.0    0.0
P             │   0.0    0.0

total : 10.0

Fij[Residue('R'), Residue('R')] # Use Residue to index the table

3.0

The function getcontingencytable allows to access the wrapped ContingencyTable in a Counts object. You can use it, in combination with normalize to get a contingency table of probabilities. The result can be wrapped inside a Probabilities object:

Probabilities(normalize(getcontingencytable(Fij)))

MIToS.Information.Probabilities{Float64, 2, MIToS.MSA.ReducedAlphabet} wrapping a MIToS.Information.ContingencyTable{Float64, 2, MIToS.MSA.ReducedAlphabet} : 

table : 8×8 Named Matrix{Float64}
Dim_1 ╲ Dim_2 │ AILMV   NQST    RHK     DE    FWY      C      G      P
──────────────┼───────────────────────────────────────────────────────
AILMV         │   0.1    0.0    0.1    0.0    0.0    0.0    0.0    0.0
NQST          │   0.0    0.1    0.0    0.0    0.0    0.0    0.0    0.0
RHK           │   0.0    0.0    0.3    0.0    0.0    0.0    0.0    0.0
DE            │   0.2    0.0    0.0    0.1    0.0    0.0    0.0    0.0
FWY           │   0.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0
C             │   0.1    0.0    0.0    0.0    0.0    0.0    0.0    0.0
G             │   0.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0
P             │   0.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0

marginals : 8×2 Named Matrix{Float64}
Residue ╲ Dim │ Dim_1  Dim_2
──────────────┼─────────────
AILMV         │   0.2    0.4
NQST          │   0.1    0.1
RHK           │   0.3    0.4
DE            │   0.3    0.1
FWY           │   0.0    0.0
C             │   0.1    0.0
G             │   0.0    0.0
P             │   0.0    0.0

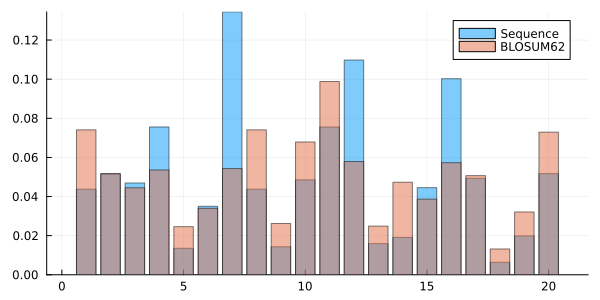
total : 1.0000000000000002

Example: Plotting the probabilities of each residue in a sequence

Similar to the count function, the probabilities function can take at least one sequence (vector of residues) and returns the probabilities of each residue. Optionally, the keyword argument alphabet could be used to count some residues in the same cell of the table.

probabilities(res"AARANHDDRDC", alphabet=alphabet)

MIToS.Information.Probabilities{Float64, 1, MIToS.MSA.ReducedAlphabet} wrapping a MIToS.Information.ContingencyTable{Float64, 1, MIToS.MSA.ReducedAlphabet} : 

table : 8-element Named Vector{Float64}
Dim_1  │ 
───────┼──────────
AILMV  │  0.272727
NQST   │ 0.0909091
RHK    │  0.272727
DE     │  0.272727
FWY    │       0.0
C      │ 0.0909091
G      │       0.0
P      │       0.0

total : 1.0

Here, we are going to use the probabilities function to get the residue probabilities of a particular sequence from UniProt.

use the getsequence function, from the MSA module, to get the sequence from a FASTA downloaded from UniProt.

julia> using MIToS.Information # to use the probabilities function
julia> using MIToS.MSA # to use getsequence on the one sequence FASTA (canonical) from UniProt
julia> seq = read("http://www.uniprot.org/uniprot/P29374.fasta", FASTA) # Small hack: read the single sequence as a MSAAnnotatedMultipleSequenceAlignment with 0 annotations : 1×1257 Named Matrix{MIToS.MSA.Residue}
                                                                                                         Seq ╲ Col │   …
───────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼──────
sp|P29374|ARI4A_HUMAN AT-rich interactive domain-containing protein 4A OS=Homo sapiens OX=9606 GN=ARID4A PE=1 SV=3 │   …
julia> probabilities(seq[1,:]) # Select the single sequence and calculate the probabilitiesMIToS.Information.Probabilities{Float64, 1, MIToS.MSA.UngappedAlphabet} wrapping a MIToS.Information.ContingencyTable{Float64, 1, MIToS.MSA.UngappedAlphabet} :

table : 20-element Named Vector{Float64}
Dim_1  │
───────┼───────────
A      │   0.043755
R      │  0.0517104
N      │  0.0469372
D      │  0.0755768
C      │  0.0135243
Q      │   0.035004
E      │   0.134447
G      │   0.043755
⋮                 ⋮
M      │  0.0159109
F      │  0.0190931
P      │  0.0445505
S      │   0.100239
T      │  0.0493238
W      │ 0.00636436
Y      │  0.0198886
V      │  0.0517104

total : 1.0

Note

In the previous example, using getsequence(seq,1) instead of seq[1,:] will return the sequence as a matrix with a single column to keep information for both dimensions. To use probabilities (or count) you can make use of the Julia's vec function to transform the matrix to a vector, e.g.: probabilities(vec(getsequence(seq,1))).

using Plots # We choose Plots because it's intuitive, concise and backend independent
gr(size=(600,300))

Plots.GRBackend()

You can plot together with the probabilities of each residue in a given sequence, the probabilities of each residue estimated with the BLOSUM62 substitution matrix. That matrix is exported as a constant by the Information module as BLOSUM62_Pi.

bar(
    1:20,
    [ frequencies  BLOSUM62_Pi ],
    lab = [ "Sequence"  "BLOSUM62"   ],
    alpha=0.5
    )

Low count corrections

Low number of observations can lead to sparse contingency tables, that lead to wrong probability estimations. It is shown in Buslje et. al. 2009 that low-count corrections, can lead to improvements in the contact prediction capabilities of the Mutual Information. The Information module has available two low-count corrections:

Additive Smoothing; the constant value pseudocount described in Buslje et. al. 2009.
BLOSUM62 based pseudo frequencies of residues pairs, similar to Altschul et. al. 1997.

using MIToS.MSA

msa = read("https://raw.githubusercontent.com/diegozea/MIToS.jl/master/docs/data/PF18883.stockholm.gz", Stockholm)

filtercolumns!(msa, columngapfraction(msa) .< 0.5) # delete columns with 50% gaps or more

column_i = msa[:,1]
column_j = msa[:,2]

811-element Named Vector{MIToS.MSA.Residue}
Seq                        │ 
───────────────────────────┼──
A0A370X5B3_9GAMM/1736-1853 │ V
D1AVB4_STRM9/461-568       │ -
A0A2T5HR93_9PSED/761-875   │ L
A0A427CBK0_9GAMM/418-540   │ -
A0A1I1MWW5_9BURK/779-907   │ -
C6JIE8_FUSVA/367-481       │ L
A0A017H8U7_9FUSO/691-802   │ L
A0A085VLZ6_PSESX/333-446   │ L
⋮                            ⋮
A0A318T6N3_9RHIZ/636-751   │ L
A0A388SGN0_9BURK/625-739   │ L
A0A443IAD3_9GAMM/1863-1969 │ -
A0A2S8VQP6_9CAUL/182-287   │ F
A0A1A9RWJ5_9NEIS/1004-1099 │ L
A6T0K2_JANMA/343-459       │ -
Q2KVL9_BORA1/480-598       │ L
A0A2W4CX06_9RHIZ/331-444   │ L

If you have a preallocated ContingencyTable you can use count! to fill it, this prevent to create a new table as count do. However, you should note that count! adds the new counts to the pre existing values, so in this case, we want to start with a table initialized with zeros.

using MIToS.Information

const alphabet = ReducedAlphabet("(AILMV)(NQST)(RHK)(DE)(FWY)CGP")

Nij = ContingencyTable(Float64, Val{2}, alphabet)

MIToS.Information.ContingencyTable{Float64, 2, MIToS.MSA.ReducedAlphabet} : 

table : 8×8 Named Matrix{Float64}
Dim_1 ╲ Dim_2 │ AILMV   NQST    RHK     DE    FWY      C      G      P
──────────────┼───────────────────────────────────────────────────────
AILMV         │   0.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0
NQST          │   0.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0
RHK           │   0.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0
DE            │   0.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0
FWY           │   0.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0
C             │   0.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0
G             │   0.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0
P             │   0.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0

marginals : 8×2 Named Matrix{Float64}
Residue ╲ Dim │ Dim_1  Dim_2
──────────────┼─────────────
AILMV         │   0.0    0.0
NQST          │   0.0    0.0
RHK           │   0.0    0.0
DE            │   0.0    0.0
FWY           │   0.0    0.0
C             │   0.0    0.0
G             │   0.0    0.0
P             │   0.0    0.0

total : 0.0

#      table  weights         pseudocount      sequences...
count!(Nij,   NoClustering(), NoPseudocount(), column_i, column_j)

MIToS.Information.ContingencyTable{Float64, 2, MIToS.MSA.ReducedAlphabet} : 

table : 8×8 Named Matrix{Float64}
Dim_1 ╲ Dim_2 │ AILMV   NQST    RHK     DE    FWY      C      G      P
──────────────┼───────────────────────────────────────────────────────
AILMV         │  30.0    0.0    0.0    0.0    3.0    0.0    0.0    0.0
NQST          │ 288.0    4.0    0.0    0.0   10.0    0.0    0.0    0.0
RHK           │  24.0    0.0    0.0    0.0    2.0    0.0    0.0    0.0
DE            │  41.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0
FWY           │   3.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0
C             │   0.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0
G             │  16.0    4.0    0.0    0.0    0.0    0.0    0.0    0.0
P             │   0.0    0.0    0.0    0.0    0.0    0.0    0.0    0.0

marginals : 8×2 Named Matrix{Float64}
Residue ╲ Dim │ Dim_1  Dim_2
──────────────┼─────────────
AILMV         │  33.0  402.0
NQST          │ 302.0    8.0
RHK           │  26.0    0.0
DE            │  41.0    0.0
FWY           │   3.0   15.0
C             │   0.0    0.0
G             │  20.0    0.0
P             │   0.0    0.0

total : 425.0

Note

You can use NoClustering() in places where clustering weights are required to not use weights. Also, NoPseudocount() in places where pseudocount values are required to not use pseudocounts.

In cases like the above, where there are few observations, it is possible to apply a constant pseudocount to the counting table. This module defines the type AdditiveSmoothing and the correspond fill! and apply_pseudocount! methods to efficiently add or fill with a constant value each element of the table.

apply_pseudocount!(Nij, AdditiveSmoothing(1.0))

MIToS.Information.ContingencyTable{Float64, 2, MIToS.MSA.ReducedAlphabet} : 

table : 8×8 Named Matrix{Float64}
Dim_1 ╲ Dim_2 │ AILMV   NQST    RHK     DE    FWY      C      G      P
──────────────┼───────────────────────────────────────────────────────
AILMV         │  31.0    1.0    1.0    1.0    4.0    1.0    1.0    1.0
NQST          │ 289.0    5.0    1.0    1.0   11.0    1.0    1.0    1.0
RHK           │  25.0    1.0    1.0    1.0    3.0    1.0    1.0    1.0
DE            │  42.0    1.0    1.0    1.0    1.0    1.0    1.0    1.0
FWY           │   4.0    1.0    1.0    1.0    1.0    1.0    1.0    1.0
C             │   1.0    1.0    1.0    1.0    1.0    1.0    1.0    1.0
G             │  17.0    5.0    1.0    1.0    1.0    1.0    1.0    1.0
P             │   1.0    1.0    1.0    1.0    1.0    1.0    1.0    1.0

marginals : 8×2 Named Matrix{Float64}
Residue ╲ Dim │ Dim_1  Dim_2
──────────────┼─────────────
AILMV         │  41.0  410.0
NQST          │ 310.0   16.0
RHK           │  34.0    8.0
DE            │  49.0    8.0
FWY           │  11.0   23.0
C             │   8.0    8.0
G             │  28.0    8.0
P             │   8.0    8.0

total : 489.0

[High level interface.] The count function has a pseudocounts keyword argument that can take a AdditiveSmoothing value to easily calculate occurrences with pseudocounts. Also the alphabet keyword argument can be used to chage the default alphabet (i.e. )

count(column_i, column_j, pseudocounts=AdditiveSmoothing(1.0), alphabet=alphabet)

MIToS.Information.Counts{Float64, 2, MIToS.MSA.ReducedAlphabet} wrapping a MIToS.Information.ContingencyTable{Float64, 2, MIToS.MSA.ReducedAlphabet} : 

table : 8×8 Named Matrix{Float64}
Dim_1 ╲ Dim_2 │ AILMV   NQST    RHK     DE    FWY      C      G      P
──────────────┼───────────────────────────────────────────────────────
AILMV         │  31.0    1.0    1.0    1.0    4.0    1.0    1.0    1.0
NQST          │ 289.0    5.0    1.0    1.0   11.0    1.0    1.0    1.0
RHK           │  25.0    1.0    1.0    1.0    3.0    1.0    1.0    1.0
DE            │  42.0    1.0    1.0    1.0    1.0    1.0    1.0    1.0
FWY           │   4.0    1.0    1.0    1.0    1.0    1.0    1.0    1.0
C             │   1.0    1.0    1.0    1.0    1.0    1.0    1.0    1.0
G             │  17.0    5.0    1.0    1.0    1.0    1.0    1.0    1.0
P             │   1.0    1.0    1.0    1.0    1.0    1.0    1.0    1.0

marginals : 8×2 Named Matrix{Float64}
Residue ╲ Dim │ Dim_1  Dim_2
──────────────┼─────────────
AILMV         │  41.0  410.0
NQST          │ 310.0   16.0
RHK           │  34.0    8.0
DE            │  49.0    8.0
FWY           │  11.0   23.0
C             │   8.0    8.0
G             │  28.0    8.0
P             │   8.0    8.0

total : 489.0

To use the conditional probability matrix BLOSUM62_Pij in the calculation of pseudo frequencies $G$ for the pair of residues $a$, $b$, it should be calculated first the real frequencies/probabilities $p_{a,b}$. The observed probabilities are then used to estimate the pseudo frequencies.

\[G_{ab} = \sum_{cd} p_{cd} \cdot BLOSUM62( a | c ) \cdot BLOSUM62( b | d )\]

Finally, the probability $P$ of each pair of residues $a$, $b$ between the columns $i$, $j$ is the weighted mean between the observed frequency $p$ and BLOSUM62-based pseudo frequency $G$, where α is generally the number of clusters or the number of sequences of the MSA and β is an empiric weight value. β was determined to be close to 8.512.

\[P_{ab} = \frac{\alpha \cdot p_{ab} + \beta \cdot G_{ab} }{\alpha + \beta}\]

This could be easily achieved using the pseudofrequencies keyword argument of the probabilities function. That argument can take a BLOSUM_Pseudofrequencies object that is created with α and β as first and second argument, respectively.

Pij = probabilities(column_i, column_j, pseudofrequencies=BLOSUM_Pseudofrequencies(nsequences(msa), 8.512))

MIToS.Information.Probabilities{Float64, 2, MIToS.MSA.UngappedAlphabet} wrapping a MIToS.Information.ContingencyTable{Float64, 2, MIToS.MSA.UngappedAlphabet} : 

table : 20×20 Named Matrix{Float64}
Dim_1 ╲ Dim_2 │           A            R  …            Y            V
──────────────┼──────────────────────────────────────────────────────
A             │  4.02435e-5    2.0553e-5  …   2.07583e-5   0.00242536
R             │  2.42108e-5    1.2343e-5      1.27929e-5   5.91367e-5
N             │  6.09849e-5   2.99208e-5      2.97281e-5    0.0630286
D             │  3.87409e-5   1.93254e-5      1.87554e-5   0.00941176
C             │  6.54375e-6   3.31392e-6      3.38733e-6   1.59938e-5
Q             │   1.9785e-5   1.01292e-5      9.78592e-6   0.00703417
E             │  2.92534e-5   1.49226e-5      1.46342e-5   7.14561e-5
G             │  3.97911e-5    2.0134e-5      1.89436e-5   0.00242091
⋮                         ⋮            ⋮  ⋱            ⋮            ⋮
M             │  7.58675e-6   3.84003e-6      3.94091e-6   1.86471e-5
F             │  1.14023e-5   5.58839e-6       5.6932e-6   0.00235792
P             │  1.21723e-5   6.16021e-6      6.20111e-6   2.98784e-5
S             │   5.3215e-5   2.68952e-5      2.67944e-5     0.028073
T             │  4.04629e-5   2.04734e-5      2.14051e-5    0.0140703
W             │  2.60994e-6   1.31427e-6      1.32588e-6   6.44815e-6
Y             │   8.8881e-6   4.45828e-6      4.49823e-6   2.21917e-5
V             │  2.10318e-5    1.0687e-5  …   1.17082e-5   5.11228e-5

marginals : 20×2 Named Matrix{Float64}
Residue ╲ Dim │       Dim_1        Dim_2
──────────────┼─────────────────────────
A             │   0.0590649  0.000497977
R             │   0.0284551  0.000251011
N             │    0.264353   0.00482829
D             │    0.065998  0.000169935
C             │ 0.000137722  0.000169793
Q             │   0.0399972   0.00483565
E             │   0.0308862  0.000221145
G             │   0.0473818  0.000233089
⋮                         ⋮            ⋮
M             │  0.00248801   0.00746638
F             │  0.00722068    0.0355818
P             │ 0.000255255  0.000151629
S             │    0.259581  0.000276161
T             │    0.142894   0.00970379
W             │  5.44982e-5   7.46526e-5
Y             │ 0.000185399  0.000252581
V             │  0.00976099     0.133954

total : 1.0

You can also use apply_pseudofrequencies! in a previously filled probability contingency table. i.e. apply_pseudofrequencies!(Pij, BLOSUM_Pseudofrequencies(α, β))

Warning

BLOSUM_Pseudofrequencies can be only be applied in normalized/probability tables with UngappedAlphabet.

Correction for data redundancy in a MSA

A simple way to reduce redundancy in a MSA without losing sequences, is clusterization and sequence weighting. The weight of each sequence should be 1/N, where N is the number of sequences in its cluster. The Clusters type of the MSA module stores the weights. This vector of weights can be extracted (with the getweight function) and used by the count and probabilities functions with the keyword argument weights. Also it's possible to use the Clusters as second argument of the function count!.

clusters = hobohmI(msa, 62) # from MIToS.MSA

MIToS.MSA.Clusters([1, 4, 4, 1, 2, 2, 2, 9, 10, 3  …  1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 2, 3, 4, 5, 6, 7, 8, 9, 10  …  297, 452, 313, 46, 140, 453, 110, 454, 423, 347], [1.0, 0.25, 0.25, 1.0, 0.5, 0.5, 0.5, 0.1111111111111111, 0.1, 0.3333333333333333  …  0.3333333333333333, 1.0, 0.5, 0.14285714285714285, 0.3333333333333333, 1.0, 0.3333333333333333, 1.0, 0.5, 0.5])

count(msa[:,1], msa[:,2], weights=clusters)

MIToS.Information.Counts{Float64, 2, MIToS.MSA.UngappedAlphabet} wrapping a MIToS.Information.ContingencyTable{Float64, 2, MIToS.MSA.UngappedAlphabet} : 

table : 20×20 Named Matrix{Float64}
Dim_1 ╲ Dim_2 │        A         R         N  …         W         Y         V
──────────────┼──────────────────────────────────────────────────────────────
A             │      0.0       0.0       0.0  …       0.0       0.0       1.0
R             │      0.0       0.0       0.0          0.0       0.0       0.0
N             │      0.0       0.0       0.0          0.0       0.0   9.27244
D             │      0.0       0.0       0.0          0.0       0.0   3.07692
C             │      0.0       0.0       0.0          0.0       0.0       0.0
Q             │      0.0       0.0  0.333333          0.0       0.0       1.5
E             │      0.0       0.0       0.0          0.0       0.0       0.0
G             │      0.0       0.0       0.0          0.0       0.0  0.333333
⋮                      ⋮         ⋮         ⋮  ⋱         ⋮         ⋮         ⋮
M             │      0.0       0.0       0.0          0.0       0.0       0.0
F             │      0.0       0.0       0.0          0.0       0.0       1.0
P             │      0.0       0.0       0.0          0.0       0.0       0.0
S             │      0.0       0.0       0.0          0.0       0.0   6.91026
T             │      0.0       0.0       0.0          0.0       0.0   3.52137
W             │      0.0       0.0       0.0          0.0       0.0       0.0
Y             │      0.0       0.0       0.0          0.0       0.0       0.0
V             │      0.0       0.0       0.0  …       0.0       0.0       0.0

marginals : 20×2 Named Matrix{Float64}
Residue ╲ Dim │    Dim_1     Dim_2
──────────────┼───────────────────
A             │     9.95       0.0
R             │      8.0       0.0
N             │  48.7224  0.333333
D             │  15.0611       0.0
C             │      0.0       0.0
Q             │  10.6429       2.0
E             │  10.1667       0.0
G             │  14.0417       0.0
⋮                      ⋮         ⋮
M             │ 0.333333       3.0
F             │      3.0   7.60794
P             │      0.0       0.0
S             │  61.5662       0.0
T             │  30.9055   2.16667
W             │      0.0       0.0
Y             │      0.0       0.0
V             │  1.16667   28.6143

total : 225.39917582417584

Estimating information measures on an MSA

The Information module has a number of functions defined to calculate information measures from Counts and Probabilities:

entropy : Shannon entropy (H)
marginal_entropy : Shannon entropy (H) of the marginals
kullback_leibler : Kullback-Leibler (KL) divergence
mutual_information : Mutual Information (MI)
normalized_mutual_information : Normalized Mutual Information (nMI) by Entropy
gap_intersection_percentage
gap_union_percentage

Information measure functions take optionally the base as the last positional argument (default: e). You can use 2.0 to measure information in bits.

using MIToS.Information
using MIToS.MSA

Ni = count(res"PPCDPPPPPKDKKKKDDGPP") # Ni has the count table of residues in this low complexity sequence

H = entropy(Ni) # returns the Shannon entropy in nats (base e)

1.327362863420189

H = entropy(Ni, 2.0) # returns the Shannon entropy in bits (base 2)

1.9149798205164812

Information module defines special iteration functions to easily and efficiently compute a measure over a MSA. In particular, mapcolfreq! and mapseqfreq! map a function that takes a table of Counts or Probabilities. The table is filled in place with the counts or probabilities of each column or sequence of a MSA, respectively. mapcolpairfreq! and mapseqpairfreq! are similar, but they fill the table using pairs of columns or sequences, respectively.

This functions take three positional arguments: the function f to be calculated, the msa and table of Counts or Probabilities.

After that, this function takes some keyword arguments:

weights (default: NoClustering()) : Weights to be used for table counting.
pseudocounts (default: NoPseudocount()) : Pseudocount object to be applied to table.
pseudofrequencies (default: NoPseudofrequencies()) : Pseudofrequencies to be applied to the normalized (probabilities) table.

mapcolpairfreq! and mapseqpairfreq! also have a fourth positional argument usediagonal that indicates if the function should be applied to identical element pairs (default to Val{true}). This two functions also have an extra keyword argument diagonalvalue (default to zero) to indicate the value used to fill the diagonal elements if usediagonal is Val{false}.

Example: Estimating H(X) and H(X, Y) over an MSA

In this example, we are going to use mapcolfreq! and mapcolpairfreq! to estimate Shannon entropy of MSA columns H(X) and the joint entropy H(X, Y) of columns pairs, respectively.

using MIToS.MSA

msa = read("https://raw.githubusercontent.com/diegozea/MIToS.jl/master/docs/data/PF18883.stockholm.gz", Stockholm)

AnnotatedMultipleSequenceAlignment with 836 annotations : 811×113 Named Matrix{MIToS.MSA.Residue}
                 Seq ╲ Col │  53   54   55   56   57  …  428  429  430  431  432
───────────────────────────┼────────────────────────────────────────────────────
A0A370X5B3_9GAMM/1736-1853 │   -    -    -    -    -  …    Y    A    Y    R    L
D1AVB4_STRM9/461-568       │   -    -    -    -    -       Y    R    Y    R    L
A0A2T5HR93_9PSED/761-875   │   S    N    L    T    S       Y    Q    Y    T    L
A0A427CBK0_9GAMM/418-540   │   -    -    -    -    -       F    R    Y    R    L
A0A1I1MWW5_9BURK/779-907   │   -    -    -    -    -       Y    E    Y    R    L
C6JIE8_FUSVA/367-481       │   -    I    I    S    N       Y    E    Y    F    L
A0A017H8U7_9FUSO/691-802   │   S    S    V    T    E       Y    E    Y    T    L
A0A085VLZ6_PSESX/333-446   │   -    -    -    -    -       Y    E    Y    Y    L
⋮                              ⋮    ⋮    ⋮    ⋮    ⋮  ⋱    ⋮    ⋮    ⋮    ⋮    ⋮
A0A318T6N3_9RHIZ/636-751   │   -    -    -    K    T       Y    V    Y    Q    L
A0A388SGN0_9BURK/625-739   │   S    E    L    T    T       Y    L    Y    E    L
A0A443IAD3_9GAMM/1863-1969 │   -    -    -    -    -       Y    D    Y    S    L
A0A2S8VQP6_9CAUL/182-287   │   -    -    -    -    R       V    R    Y    R    -
A0A1A9RWJ5_9NEIS/1004-1099 │   S    T    V    T    N       -    -    -    -    -
A6T0K2_JANMA/343-459       │   -    -    -    -    -       Y    A    Y    T    L
Q2KVL9_BORA1/480-598       │   S    R    I    T    R       Y    E    Y    R    L
A0A2W4CX06_9RHIZ/331-444   │   -    -    -    -    N  …    Y    E    Y    L    L

We are going to count residues to estimate the entropy. The entropy estimation is performed over a rehused Counts object. The result will be a vector containing the values estimated over each column without counting gaps (UngappedAlphabet).

using MIToS.Information

Hx = mapcolfreq!(entropy, msa, Counts(ContingencyTable(Float64, Val{1}, UngappedAlphabet())))

1×113 Named Matrix{Float64}
Function ╲ Col │        53         54  …        431        432
───────────────┼──────────────────────────────────────────────
entropy        │      -0.0    2.28908  …    2.43627       -0.0

If we want the joint entropy between columns pairs, we need to use a bidimensional table of Counts and mapcolpairfreq!.

Hxy = mapcolpairfreq!(entropy, msa, Counts(ContingencyTable(Float64, Val{2}, UngappedAlphabet())))

113×113 Named PairwiseListMatrices.PairwiseListMatrix{Float64, true, Vector{Float64}}
Col1 ╲ Col2 │        53         54  …        431        432
────────────┼──────────────────────────────────────────────
53          │      -0.0    2.27907  …    2.34531       -0.0
54          │   2.27907    2.28908       4.19681    2.25097
55          │   1.12284     3.2452       3.37893    1.14042
56          │   1.77041    3.76691        4.0201    2.04439
57          │   2.18455    4.03923       4.17225    2.07303
58          │  0.570446    2.76359       3.06398   0.779658
59          │   2.11739     4.0329       4.28252    2.19535
60          │   1.53981    3.46025       3.35723    1.08494
⋮                     ⋮          ⋮  ⋱          ⋮          ⋮
423         │   1.09798    3.13026       3.42102    1.19229
424         │  0.479167    2.61361       2.62843   0.258226
427         │   1.34976    3.38375       3.37444    1.13379
428         │  0.600381    2.79541       3.06003   0.721655
429         │   1.52338    3.49462       3.90651    1.86877
430         │ 0.0584063     2.3272        2.4817  0.0594665
431         │   2.34531    4.19681       2.43627    2.40596
432         │      -0.0    2.25097  …    2.40596       -0.0

In the above examples, we indicate the type of each occurrence in the counting and the probability table to use. Also, it's possible for some measures as entropy and mutual information, to estimate the values only with the count table (without calculate the probability table). Estimating measures only with a ResidueCount table, when this is possible, should be faster than using a probability table.

Time_Pab = map(1:100) do x
    time = @elapsed mapcolpairfreq!(entropy, msa, Probabilities(ContingencyTable(Float64, Val{2}, UngappedAlphabet())))
end

Time_Nab = map(1:100) do x
    time = @elapsed mapcolpairfreq!(entropy, msa, Counts(ContingencyTable(Float64, Val{2}, UngappedAlphabet())))
end

using Plots
gr()

histogram( [Time_Pab Time_Nab],
    labels = ["Using ResidueProbability" "Using ResidueCount"],
    xlabel = "Execution time [seconds]" )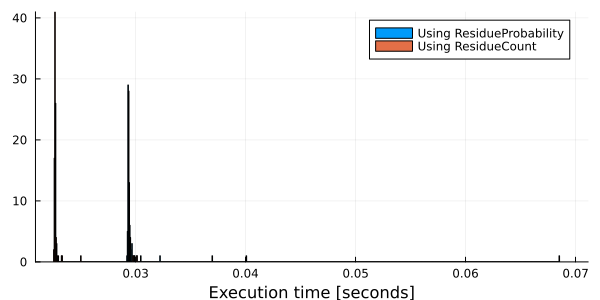

Corrected Mutual Information

MIToS ships with two methods to easily calculate corrected mutual information. The first is the algorithm described in Buslje et. al. 2009. This algorithm can be accessed through the buslje09 function and includes:

Low count correction using AdditiveSmoothing
Sequence weighting after a hobohmI clustering
Average Product Correction (APC) proposed by

Dunn et. al. 2008, through the APC! function that takes a MI matrix.

Z score correction using the functions shuffle! from the MSA module and zscore

from the PairwiseListMatrices package.

MIToS.Information.buslje09 — Function

buslje09 takes a MSA or a file and a FileFormat as first arguments. It calculates a Z score and a corrected MI/MIp as described on Busjle et. al. 2009.

keyword argument, type, default value and descriptions:

  - lambda      Float64   0.05    Low count value
  - clustering  Bool      true    Sequence clustering (Hobohm I)
  - threshold             62      Percent identity threshold for clustering
  - maxgap      Float64   0.5     Maximum fraction of gaps in positions included in calculation
  - apc         Bool      true    Use APC correction (MIp)
  - samples     Int       100     Number of samples for Z-score
  - fixedgaps   Bool      true    Fix gaps positions for the random samples
  - alphabet    ResidueAlphabet UngappedAlphabet()  Residue alphabet to be used

This function returns:

  - Z score
  - MI or MIp

source

The second, implemented in the BLMI function, has the same corrections that the above algorithm, but use BLOSUM62 pseudo frequencies. This function is slower than buslje09 (at the same number of samples), but gives better performance (for structural contact prediction) when the MSA has less than 400 clusters after a Hobohm I at 62% identity.

MIToS.Information.BLMI — Function

BLMI takes a MSA or a file and a FileFormat as first arguments. It calculates a Z score (ZBLMI) and a corrected MI/MIp as described on Busjle et. al. 2009 but using using BLOSUM62 pseudo frequencies instead of a fixed pseudocount.

Keyword argument, type, default value and descriptions:

  - beta        Float64   8.512   β for BLOSUM62 pseudo frequencies
  - lambda      Float64   0.0     Low count value
  - threshold             62      Percent identity threshold for sequence clustering (Hobohm I)
  - maxgap      Float64   0.5     Maximum fraction of gaps in positions included in calculation
  - apc         Bool      true    Use APC correction (MIp)
  - samples     Int       50      Number of samples for Z-score
  - fixedgaps   Bool      true    Fix gaps positions for the random samples

This function returns:

  - Z score (ZBLMI)
  - MI or MIp using BLOSUM62 pseudo frequencies (BLMI/BLMIp)

source

Example: Estimating corrected MI from an MSA

using MIToS.MSA
using MIToS.Information

msa = read("https://raw.githubusercontent.com/diegozea/MIToS.jl/master/docs/data/PF18883.stockholm.gz", Stockholm)
ZMIp, MIp  = buslje09(msa)
ZMIp

107×107 Named PairwiseListMatrices.PairwiseListMatrix{Float64, false, Vector{Float64}}
Col1 ╲ Col2 │          57           58  …          431          432
────────────┼──────────────────────────────────────────────────────
57          │         NaN      3.80558  …      1.22929     -1.61299
58          │     3.80558          NaN        -2.69685       4.3832
59          │     4.12852      3.09853         3.02155      -2.3654
60          │     1.28128      3.53636        -3.24632      1.37996
61          │     3.37026      1.11025        0.735821     -1.17246
64          │     1.07316      4.06038        -2.66907      4.77842
65          │    0.153152     -1.18427        0.906491     -2.21183
66          │    0.282086      3.95033        -3.37113      2.84446
⋮                       ⋮            ⋮  ⋱            ⋮            ⋮
423         │    0.607208     -1.65247      -0.0624896    -0.809143
424         │     1.41374      1.68355        -2.40346      4.61623
427         │     1.16704    -0.579281         2.11878     0.228299
428         │    -2.11596      2.43479        -1.50752      3.82858
429         │    0.186837     -1.61496         7.00909     -1.00025
430         │    -1.64697      2.66322        -2.85505      7.32344
431         │     1.22929     -2.69685             NaN     -3.13229
432         │    -1.61299       4.3832  …     -3.13229          NaN

ZBLMIp, BLMIp  = BLMI(msa)
ZBLMIp

107×107 Named PairwiseListMatrices.PairwiseListMatrix{Float64, false, Vector{Float64}}
Col1 ╲ Col2 │           57            58  …           431           432
────────────┼──────────────────────────────────────────────────────────
57          │          NaN    -0.0058753  …      0.054706   -0.00724753
58          │   -0.0058753           NaN      -0.00230327     0.0093646
59          │  -0.00462501     0.0177384        0.0716935   -0.00916293
60          │   -0.0385254     0.0114635       -0.0411778    0.00585093
61          │    0.0076633   -0.00767814        0.0146958   -0.00519354
64          │    0.0070737    0.00620751        -0.005128     0.0122708
65          │    -0.046307    -0.0287545       0.00846159    -0.0071145
66          │    -0.018272     0.0306033       -0.0277811    0.00521656
⋮                        ⋮             ⋮  ⋱             ⋮             ⋮
423         │     0.030699    -0.0166871       -0.0186436   -0.00203097
424         │    0.0653332    -0.0104712       -0.0142883    0.00839156
427         │    0.0409193    -0.0109902        0.0254383  -0.000165967
428         │   -0.0293523     0.0176844      -0.00865934     0.0105738
429         │    0.0123588    -0.0182636        0.0861102   -0.00345761
430         │   -0.0202489   -0.00581871       -0.0176394     0.0242715
431         │     0.054706   -0.00230327              NaN   -0.00883419
432         │  -0.00724753     0.0093646  …   -0.00883419           NaN

Visualize Mutual Information

You can use the function of the Plots package to visualize the Mutual Information (MI) network between residues. As an example, we are going to visualize the MI between residues of the Pfam domain PF18883. The heatmap is the simplest way to visualize the values of the Mutual Information matrix.

using Plots
gr()

heatmap(ZMIp, yflip=true)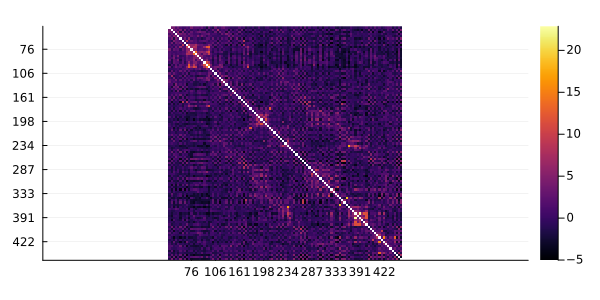

ZMIp is a Z score of the corrected MIp against its distribution on a random MSA (shuffling the residues in each sequence), so pairs with highest values are more likely to co-evolve. Here, we are going to use the top 1% pairs of MSA columns.

using PairwiseListMatrices # to use getlist
using Statistics # to use quantile

threshold = quantile(getlist(ZMIp), 0.99)

7.0709810753695335

ZMIp[ ZMIp .< threshold ] .= NaN
heatmap(ZMIp, yflip=true)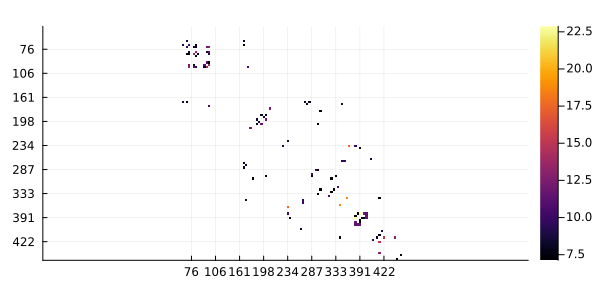

We are going to calculate the cMI (cumulative mutual information) value of each node. Where cMI is a mutual information score per position that characterizes the extent of mutual information "interactions" in its neighbourhood. This score is calculated as the sum of MI values above a certain threshold for every amino acid pair where the particular residue appears. This value defines to what degree a given amino acid takes part in a mutual information network and we are going to indicate it using the node color. To calculate cMI we are going to use the cumulative function:

cMI = cumulative(ZMIp, threshold)

1×107 Named Matrix{Float64}
Function ╲ Col2 │      57       58       59  …      430      431      432
────────────────┼────────────────────────────────────────────────────────
cumulative      │     0.0      0.0      0.0  …  7.32344      0.0  7.32344